Question

You drop a 3.00 kg book to a friend who stands on the ground at distance D = 14.0 m below. If your friend's outstretched hands are at distance d = 1.30 m above the ground (see the figure), (a) how much work Wg does the gravitational force do on the book as it drops to her hands? (b) What is the change ΔU in the gravitational potential energy of the book-Earth system during the drop? If the gravitational potential energy U of that system is taken to be zero at ground level, what is U (c) when the book is released and (d) when it reaches her hands? Now take U to be 100 J at ground level and again find (e) Wg, (f ) ΔU, (g) U at the release point, and (h) U at her hands.

Answer 1

(a) 373.4 J

The displacement of the book is

`d=14.0 m - 1.30 m=12.7 m`

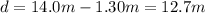
While the gravitational force acting on the book is

`F=mg=(3.00 kg)(9.8 m/s^2)=29.4 N`

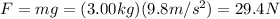
And the force (downward) is parallel to the displacement (downward), so the work done by gravity is

`W=Fd=(29.4 N)(12.7 m)=373.4 J`

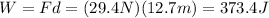
(b) -373.4 J

The work done by the Earth on the book has been converted into kinetic energy of the book (because the book accelerates as it approaches the ground). SInce the total mechanical energy of the Earth-book system must be conserved, this means that potential energy U has been converted into kinetic energy K: therefore, the loss in potential energy U is exactly -373.4 J.

(c) 411.6 J

The gravitational potential energy U is given by:

`U=mgh`

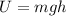
where m = 3.00 kg is the mass of the book, g = 9.8 m/s^2 is the gravitational acceleration, h=14.0 m is the height of the book above the reference level (the ground). Substituting,

`U=(3.00 kg)(9.8 m/s^2)(14.0 m)=411.6 J`

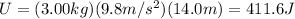
(d) 38.2 J

When the book reaches the hand, its height above the ground level is

h = 1.30 m

therefore, the gravitational potential energy this time is

`U=mgh=(3.00 kg)(9.8 m/s^2)(1.30 m)=38.2 J`

(e) 373.4 J

The work done by gravity does not change if we change the value of the potential energy at ground level. In fact, the work done by gravity is still calculated as before:

`W=Fd=(29.4 N)(12.7 m)=373.4 J`

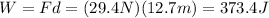
(f) -373.4 J

As we did in point b), the work done by the Earth on the book has been converted into kinetic energy of the book (because the book accelerates as it approaches the ground), so the loss in potential energy is equal to the work done by gravity, and this value does not depend on the value of the potential energy at ground level, so it is still -373.4 J.

(g) 511.6 J

The gravitational potential energy U is given by:

`U=mgh+U_0`

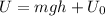
where m = 3.00 kg is the mass of the book, g = 9.8 m/s^2 is the gravitational acceleration, h=14.0 m is the height of the book above the reference level (the ground), and
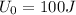`U_0 = 100 J` is the potential energy at ground level, which must be added into the formula. Substituting,

`U=(3.00 kg)(9.8 m/s^2)(14.0 m)+100 J=511.6 J`

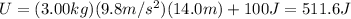
(h) 138.2 J

As before, we can calculate the potential energy of the book at a height of h=1.30 m, adding 100 J of energy which is the value of the potential energy at ground level. we find:

`U=mgh+U_0=(3.00 kg)(9.8 m/s^2)(1.30 m)+100 J=138.2 J`