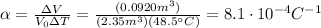Answer:
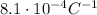
Step-by-step explanation:
The volumetric expansion of the liquid is given by
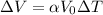
where
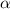 is the coefficient of volume expansion
is the coefficient of volume expansion
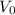 is the initial volume
is the initial volume
 is the change in temperature
is the change in temperature
For the liquid in this problem,
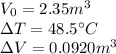
So we can solve the equation to find
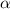 :
: