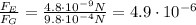Question

A bumblebee flying through the air picks up a net charge of +40 pC, due in part to the triboelectric effect (charge transfer by friction) from collision with small dust particles*. The presence of this positive charge on their bodies helps the bumblebees locate negatively charged flowers when foraging for pollen and nectar**. The natural electric field near the surface of the Earth has an average magnitude of 120 N/C and is directed downward. The mass of a typical bumblebee is 0.10 grams. Calculate the ratio of the Coulomb force on the bee to the gravitational force on the bee. Note that (1pC = 10^{-12} C)(1pC=10 ​−12 ​​ C). [For small number answers, use the scientific “E” notation : 0.0076 = 7.6E-3 ]

Answer 1

`4.9\cdot 10^(-6)`

Step-by-step explanation:

The Coulomb force on the bee is:

`F_E=qE`

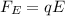
where

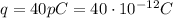`q=40 pC=40\cdot 10^(-12) C` is the charge of the bee

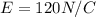`E=120 N/C` is the magnitude of the electric field

Substituting into the formula,

`F_E=(40\cdot 10^(-12) C)(120 N/C)=4.8\cdot 10^(-9) N`

The gravitational force on the bee is

`F_G = mg`

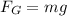
where

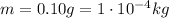`m=0.10 g=1\cdot 10^(-4)kg` is the bee's mass

`g=9.8 m/s^2` is the gravitational acceleration

Substituting into the formula,

`F_G = mg=(1\cdot 10^(-4)kg)(9.8 m/s^2)=9.8\cdot 10^(-4) N`

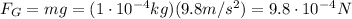
So, the ratio between the two forces is

`(F_E)/(F_G)=(4.8\cdot 10^(-9) N)/(9.8\cdot 10^(-4) N)=4.9\cdot 10^(-6)`