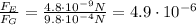Answer:
Step-by-step explanation:
The Coulomb force on the bee is:
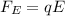
where
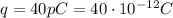 is the charge of the bee
is the charge of the bee
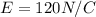 is the magnitude of the electric field
is the magnitude of the electric field
Substituting into the formula,
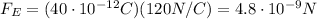
The gravitational force on the bee is
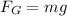
where
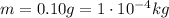 is the bee's mass
is the bee's mass
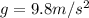 is the gravitational acceleration
is the gravitational acceleration
Substituting into the formula,
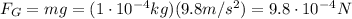
So, the ratio between the two forces is