Hello!
The answer is:
There are needed 46.67 liters of the 30% solution and 23.33 liters of the 60% solution in order to make 70 liters of a 40% solution.
Why?
We can solve this problem creating a system of equations. Let's make the two equations that will help us to solve the problem.
From the statement we know that a solution of 70 liters of a 40% is needed, and there are two differents solutions available, of 30% and 60% and we need to use them to make 70 liters of a 40% solution, so:
So:

If both solutions will make a 70 liters solution, so the first equation will be:
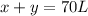
Let's work with real numbers converting the percent values into real numbers by dividing it into 100, so:

Then, we know that both solutions will make 70 liters of a 40% solution, so the second equation will be:
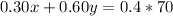
Therefore, from the first equation we have:
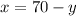
Then, substituting x into the second equation to find y, we have:
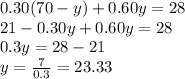
Hence, substituting y into the first equation to find x, we have:

So, there are needed 46.67 liters of the 30% solution and 23.33 liters of the 60% solution in order to make 70 liters of a 40% solution.
Have a nice day!