Question

a scientist is growing bacteria in a lab for study one particular type of bacteria grows at a rate of y=2t^2+3t+500 a different bacteria grows at a rate of y=3t^2+t+300 in both of these eqiations y is the number of bacteria after t minutes when is there an equal number of both types of bacteria

Answer 1

ANSWER

t=15 minutes.

Step-by-step explanation

The equation that models the growth rate of the first type of bacteria is,


`y = 2 {t}^(2) + 3t + 500`

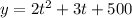
The growth rate of a second type of bacteria is modeled by:


`y = 3 {t}^(2) + t + 300`

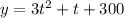
Since y is the number of bacteria after t minutes in both equations, we equate both equations to find the time when there is an equal number of both types of bacteria.


`3 {t}^(2) + t + 300 = 2 {t}^(2) + 3t + 500`

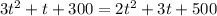
We rewrite as standard quadratic equation,


`3 {t}^(2) - 2 {t}^(2) + t - 3t + 300 - 500 = 0`


`{t}^(2) - 2t - 200 = 0`

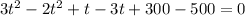
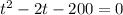
We use the quadratic formula to obtain,


`t = \frac{ - - 2 \pm \sqrt{ {( - 2)}^(2) - 4(1)( - 200) } }{2(1)}`


`t = ( -2 \pm √( 804) )/(2)`


`t = ( -2 \pm 2√( 201) )/(2)`


`t = 1 - √(201) \: or \: t = 1 + √(201)`

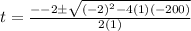
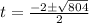
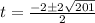
t=-13.177 or t=15.177

We discard the negative value. Hence there is an equal number of both types of bacteria after approximately 15 minutes.