Answer:
The point is (3.5 , 7.25)
Explanation:
∵ A = (2 , 8) and B = (8 , 5)
∵ Let point P divides AB into a ratio 1:3
∵

∵
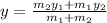
∴ x-coordinate of P = (2)(3) + (8)(1)/3 + 1 = (6 + 8)/4 = 3.5
∴ y-coordinate of P = (8)(3) + (5)(1)/1 + 3 = (24 + 5)/4 = 7.25
∴ P = (3.5 , 7.25)