The length of the missing side is √445 meters.
For a right triangle, the Pythagorean theorem states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (the legs).
In this case, we are given the lengths of the two legs, which are 11 meters and 18 meters. We need to find the length of the hypotenuse, which is the missing side.
Steps to solve:
Step 1: Substitute the given values into the Pythagorean theorem:
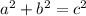
where:
a = 11 meters (shorter leg)
b = 18 meters (longer leg)
c = the missing side (hypotenuse)
Step 2: Evaluate the equation:
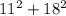 =
=
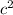
121 + 324 =
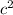
445 =
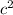
Step 3: Take the square root of both sides to solve for c:
c = √445
The length of the missing side is √445 meters