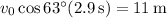Question

I can’t figure this out!!! Answer what you can , please.

A soccer player kicks a ball from the ground with a speed of 16 m/s at an angle of 63°.

A. What is the horizontal component of the velocity?
B. What is the vertical component of the velocity?
C. How long does it take the ball to reach its highest point?
D. What is the maximum height of the ball?
E. What is the total time that the ball is in the air?
F. How far is the ball from the soccer player when it lands?

Answer 1

a/b. The ball has velocity vector at time
`t`

`\vec v=(v_x,v_y)=(v_0\cos63^\circ,v_0\sin63^\circ-gt)`

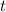
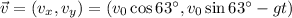
where
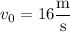`v_0=16(\rm m)/(\rm s)` is the ball's initial speed and
`g=9.8(\rm m)/(\mathrm s^2)`.

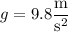c. At its highest point, the ball has 0 vertical speed. This occurs when

`v_0\sin63^\circ-gt=0\implies t=1.5\,\mathrm s`

d. Recall that

`{v_y}^2-{v_(0y)}^2=-2g\Delta y`

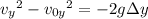
so that at its highest point,

`0^2-(v_0\sin63^\circ)^2=-2g\Delta y\implies\Delta y=10\,\mathrm m`

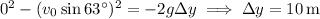
e. This is just twice the time it takes for the ball to reach its maximum height,
`t=2.9\,\mathrm s`.

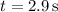f. The ball's horizontal position after time
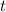`t` is

`v_0\cos63^\circ\,t`

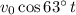
so that after the time found in part (f), the ball has traveled

`v_0\cos63^\circ(2.9\,\mathrm s)=11\,\mathrm m`