Question

Please help!!!!!!!!!

Answer 1

Hello!

The answer is:

C.
`(x-√(5x))/(x-5)`

Why?

Since we have rational numbers on both numerator and denominator, we need to rationalize (simplify) using the conjugate method on the denominator, for this case, the conjugate will be the same expression changing the positive sign "+" to a negative sign "-". Conjugate method means that we need to multiply and divide for the same term in order to not affect the expression.

Also, for solving this problem, we need to remember the following:

`a^(2)-b^(2)=(a+b)(a-b)`

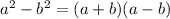
And,

`\sqrt[n]{a}*\sqrt[n]{b}=\sqrt[n]{a*b}`

So, the conjugate for the expression will be:

`√(x)-√(5)`

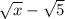
Applying the conjugate for the expression, we will have:

`(√(x) )/(√(x)+√(5))*(√(x)-√(5))/(√(x)-√(5))=(√(x)*√(x) -√(x)*√(5))/((√(x))^(2)-√(x)*√(5)+√(5)*√(x)-(√(5))^(2))\\\\((√(x))^(2)-√(5x))/(x-5)=(x-√(5x))/(x-5)`

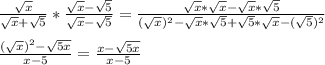
So, the rationalized form of the expression is:

`(x-√(5x))/(x-5)`

Have a nice day!