Answer:

Explanation:
Here given measure of sides are 18 , 24 and 30 units. Firstly let's find the area of ∆ using Heron's Formula.
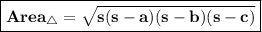
Where s is semi Perimeter . And here s will be ( 18 + 24 + 30 ) / 2 = 36 units .
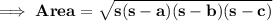
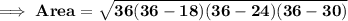
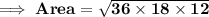
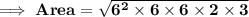
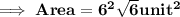
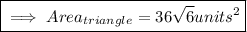
Also we know that ,
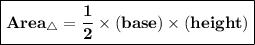
Let's find the altitudes now ,
Altitude on side of 18 units :-

Altitude on side of 24 units :-

Altitude on side 30 units :-

Hence the lenght of shortest altitude is 2.4√6 units and its on the side of 30 units.