Question

PLZZZZZZ NEED HELP!!!!!!!

Answer 1

A formula known as law of cosine (sometimes also referred to as Carnot's rule) states that, in any triangle ABC, you have

`\overline{AB}^2 = \overline{BC}^2+\overline{AC}^2-2\overline{AC}\overline{BC}\cos(\alpha)`

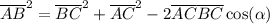
where
`\alpha` is the angle between AC and BC. This formula generalizes Pythagoras' theorem, since it doesn't require the triangle to be right. In your case, we have

`[tex]AB = \sqrt{(1)/(4)+(1)/(9)-2\cdot(1)/(2)\cdot(1)/(3)\cdot\cos(100)} = \sqrt{(13)/(36)-(\cos(100))/(3)} \approx 0.65`

Answer 2

a^2 + b^2= c^2. Aka 1/2*1/2 (1/4) + 1/3*1/3 (1/9)= (13/36) is your answer squared.

Square root of 13/36 is 0.10015420209 but to simplify to the nearest hundred it is 0.10.