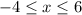Answer:
See attachment
Explanation:
The given parametric equations are;
 and
and
 ,
,
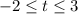 .
.
We can graph this by plotting some few points within the given range or eliminate the parameter to identify the type of curve.
Plotting points;
When
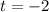 ,
,
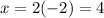 and
and
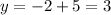
This gives the point (-4,3).
When

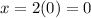 and
and
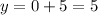
This gives the point (0,5).
When
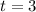
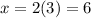 and
and
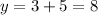
This gives the point (6,8).
We plot these points and draw a straight line through them.
Eliminating the parameter.


Make t the subject in the second equation;

Substitute into the first equation;
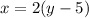
This implies that;

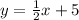
This is an equation of a straight line with slope
 and y-intercept 5 on the interval
and y-intercept 5 on the interval