Answer:
D) constant negative acceleration
Step-by-step explanation:
Acceleration is defined as the ratio of changing of the velocity per unit time:
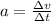
where v is the velocity and t the time.
In a velocity-time graph, as the one above, the ratio between change in velocity and change in time corresponds to the slope of the curve. In fact, the slope of the curve is defined as
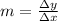
where
 is the increment in the y-variable, which corresponds to the change in the velocity,
is the increment in the y-variable, which corresponds to the change in the velocity,

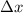 is the increment in the x-variable, which corresponds to the change in the time,
is the increment in the x-variable, which corresponds to the change in the time,
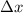
So, since the slope in this case is 1) constant and 2) negative, this means that the acceleration is also constant and negative.