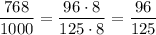The decimal representation of any number is a linear combination of powers of 10. In other words, given a number like 123.456, we can expand it as
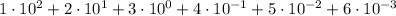
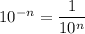 for any
for any
 , so the above is the same as
, so the above is the same as
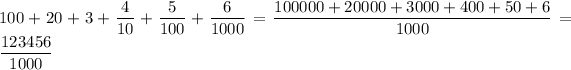
Similarly, we can write
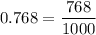
Now it's a question of reducing the fraction as much as possible. We have
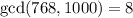 so
so