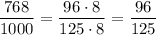1 Answer

Dan Schnau · Answer 1 · 2020-09-25T23:38:16+0000

The decimal representation of any number is a linear combination of powers of 10. In other words, given a number like 123.456, we can expand it as

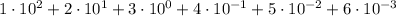
$1\cdot10^2+2\cdot10^1+3\cdot10^0+4\cdot10^(-1)+5\cdot10^(-2)+6\cdot10^(-3)$

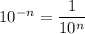$10^(-n)=\frac1{10^n}$ for any
, so the above is the same as

$100+20+3+\frac4{10}+\frac5{100}+\frac6{1000}=(100000+20000+3000+400+50+6)/(1000)=(123456)/(1000)$

Similarly, we can write

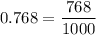
0.768=(768)/(1000)

Now it's a question of reducing the fraction as much as possible. We have
$\mathrm{gcd}(768,1000)=8$ so

$(768)/(1000)=(96\cdot8)/(125\cdot8)=(96)/(125)$

Please log in or register to add a comment.