Question

Find (f o f) (3) . f(x)= x^2-x

Answer 1

(f º f)(3) = 30, when f(x) = x² - x

Explanation:

This is a great example of composite functions and how to multiply one function by another. (f º f) really means f(f(x)), or replacing every x in the original function f(x) with the function f(x).

Step 1: State the original function.

`f(x) = x^(2) -x`

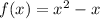
Step 2: Insert the function f(x) wherever there is an x.

`f(f(x))=(x^(2) -x)^(2) -(x^2-x)`

Step 3: Expand anything that has an exponent. Remember:
`(x+y)^2 = (x+y)(x+y)`

`f(f(x))=(x^(2) -x)(x^(2) -x) -(x^2-x)`

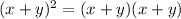
Step 4: Foil the parts of the equations in brackets by multiplying the first terms, outside terms, inside terms and last terms in each bracket.

`f(f(x))=(x^(4)-x^3-x^3+x^(2)) -(x^2-x)`

Step 5: Now you can remove the brackets (don'f forget to switch the symbols for the second brackets because you are subtracting) and sum the like terms.

`f(f(x))=x^(4)-x^3-x^3+x^(2) -x^2+x`

`f(f(x))=x^(4)-2x^3+x`

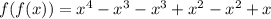
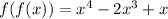
Step 6: Finally, substitute the given x value, which is 3, into the new equation.

`f(f(x))=(3)^(4)-2(3)^3+(3)`

`f(f(x))=81-54+3`

`f(f(x))=30`

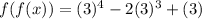
Therefore the answer is (f º f)(3) = 30.

Answer 2

30

Explanation:

Method 1:

ƒ(x) = x² - x

(f∘f)(x) = f(f(x)) = f(x²-x) = (x² - x)² - (x² - x) = x⁴ - 2x³ + x² - x² + x = x⁴ - 2x³ + x

(f∘f)(3) = 3⁴ - 2(3)³ + 3 = 81 - 54 + 3 = 30

Method 2:

f(3) = 3² - 3 = 9 - 3 = 6

(f∘f)(3) = f(f(3)) = f(6) = 6² - 6 = 36 - 6 = 30