Question

asked May 26, 2022 177k views

2 Answers

Murakami · Answer 1 · 2022-05-29T19:06:30+0000

The matrix is not properly formatted.

However, I'm able to rearrange the question as:

$\left[\begin{array}{ccc}1&1&1|-1\\-2&3&5|3\\3&2&4|1\end{array}\right]$

Operations:

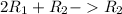
2R_1 + R_2 ->R_2

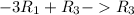
-3R_1 +R_3 ->R_3

Please note that the above may not reflect the original question. However, you should be able to implement my steps in your question.

Answer:

$\left[\begin{array}{ccc}1&1&1|-1\\0&5&7|1\\0&-1&1|4\end{array}\right]$

Explanation:

The first operation:

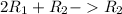
2R_1 + R_2 ->R_2

This means that the new second row (R2) is derived by:

Multiplying the first row (R1) by 2; add this to the second row

The row 1 elements are:

$\left[\begin{array}{ccc}1&1&1|-1\end{array}\right]$

Multiply by 2

$2 * \left[\begin{array}{ccc}1&1&1|-1\end{array}\right] = \left[\begin{array}{ccc}2&2&2|-2\end{array}\right]$

Add to row 2 elements are:
$\left[\begin{array}{ccc}-2&3&5|3\end{array}\right]$

$\left[\begin{array}{ccc}2&2&2|-2\end{array}\right] + \left[\begin{array}{ccc}-2&3&5|3\end{array}\right]$

$\left[\begin{array}{ccc}0&5&7|1\end{array}\right]$

The second operation:

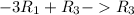
-3R_1 +R_3 ->R_3

This means that the new third row (R3) is derived by:

Multiplying the first row (R1) by -3; add this to the third row

The row 1 elements are:

$\left[\begin{array}{ccc}1&1&1|-1\end{array}\right]$

Multiply by -3

$-3 * \left[\begin{array}{ccc}1&1&1|-1\end{array}\right] = \left[\begin{array}{ccc}-3&-3&-3|3\end{array}\right]$

Add to row 2 elements are:
$\left[\begin{array}{ccc}3&2&4|1\end{array}\right]$

$\left[\begin{array}{ccc}-3&-3&-3|3\end{array}\right] + \left[\begin{array}{ccc}3&2&4|1\end{array}\right]$

$\left[\begin{array}{ccc}0&-1&1|4\end{array}\right]$

Hence, the new matrix is:

$\left[\begin{array}{ccc}1&1&1|-1\\0&5&7|1\\0&-1&1|4\end{array}\right]$

Please log in or register to add a comment.