Question

The product of (4z^2 + 7z - 8) and (-z + 3) is -4z^3 + xz^2 + yz - 24. What is the value of x? What is the value of y?

Answer 1

x = 5

y = 29

Explanation:

Edge Answer

Answer 2

`x=5+(29)/(z)-(y)/(z)`

`y=5z+29-xz`

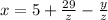
Explanation:

Given:
`(4z^2+7z-8)(-z+3)=-4z^3+xz^2+yz-24`; find x and y.

Let's start with finding x first. Let's distribute the left side of the equation.

`-4z^3+5z^2+29z-24=-4z^3+xz^2+yz-24`

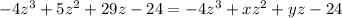
Let's move everything we can to the left side of the equation. Some things will cancel out.

`5z^2+29z=xz^2+yz`

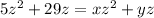
Now, let's move the term that includes
`x` to the left side of the equation. Everything else should be moved to the right.

`-xz^2=-5z^2-29z+yz`

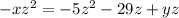
Let's get rid of the negative sign in front of
`x` by dividing both sides by -1.

`xz^2=5z^2+29z-yz`

To get
`x` completely isolated, divide both sides by
`z^2`.

`(xz^2)/(z^2)=(5z^2)/(z^2)+(29z)/(z^2)-(yz)/(z^2)`

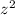Simplify.

`x=5+(29)/(z)-(y)/(z)`

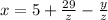
Let's solve for y. We will start with the distributed and simplified equation to make it easier.

`5z^2+29z=xz^2+yz`

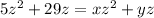
Now, let's move the term that includes
`y` to the left side of the equation. Everything else should be moved to the right.

`-yz=-5z^2-29z+xz^2`

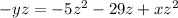
Again, let's get rid of the negative sign in front of the
`y` by dividing both sides by -1.

`yz=5z^2+29z-xz^2`

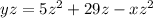
To isolate y, divide both sides by z.

`(yz)/(z)=(5z^2)/(z)+(29z)/(z)-(xz^2)/(z)`

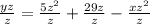
Simplify.

`y=5z+29-xz`