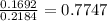Answer:
77.47%
Explanation:
We have to use Bayes Theorem in solving this problem.
This theorem's formula is:
P(A | B) =
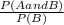
Where the " | " means "given that".
For our problem, using bayes theorem, we can write:
P(Student has lice | positive ) =
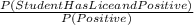
- P(Positive) = 0.1692 + 0.0492 = 0.2184
- P (Student has Lice & Positive ) = 0.1692
So P(Student has lice | Positive ) =