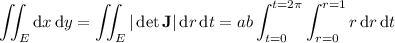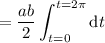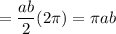Question

Definite Integrals Calculus. Can someone help me on where to get started with this. Prove the area of this ellipse

Answer 1

If you already know some multivariable calculus, you can simply compute the double integral

`\displaystyle\iint_E\mathrm dx\,mathrm dy`

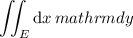
where
`E` denotes the region bounded by the ellipse with equation

`(x^2)/(a^2)+(y^2)/(b^2)=1`

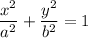
We can solve for
`y`:

`y=\pm\sqrt{b^2-(b^2x^2)/(a^2)}=\pm\frac ba√(a^2-x^2)`

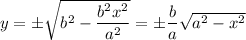
then the integral becomes

`\displaystyle\int_(x=-a)^(x=a)\int_(y=-\frac ba√(a^2-x^2))^(y=\frac ba√(a^2-x^2))\mathrm dy\,\mathrm dx`

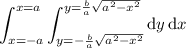
We also could have solve for
`x` instead and swapped the order of integration, so that the area is

`\displaystyle\int_(y=-b)^(y=b)\int_(x=-\frac ab√(b^2-y^2))^(x=\frac ab√(b^2-y^2))\mathrm dx\,\mathrm dy`

If you don't know about double integrals yet, these basically reduce to either of the single-variate integrals,

`\displaystyle\frac{2b}a\int_(x=-a)^(x=a)√(a^2-x^2)\,\mathrm dx=\frac{4b}a\int_(x=0)^(x=a)√(a^2-x^2)\,\mathrm dx`

(making use of the fact that
`√(a^2-x^2)` is symmetric about 0) or

`\displaystyle\frac{2a}b\int_(y=-b)^(y=b)√(b^2-y^2)\,\mathrm dx=\frac{4a}b\int_(y=0)^(y=b)√(b^2-y^2)\,\mathrm dy`

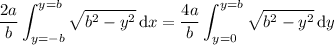
either of which can be evaluated with a trigonometric substitution. For instance, taking
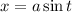`x=a\sin t`, gives
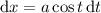`\mathrm dx=a\cos t\,\mathrm dt`, and the integral becomes

`\displaystyle\frac{4b}a\int_(a\sin t=0)^(a\sin t=a)√(a^2-(a\sin t)^2)\,a\cos t\,\mathrm dt=4ab\int_(t=0)^(t=\pi/2)√(1-\sin^2t)\cos t\,\mathrm dt`

`=\displaystyle4ab\int_(t=0)^(t=\pi/2)\cos^2t\,\mathrm dt`

`=\displaystyle2ab\int_(t=0)^(t=\pi/2)(1+\cos2t)\,\mathrm dt`

`=2ab\left(t+\frac12\sin2t\right)\bigg|_(t=0)^(t=\pi/2)`

`=2ab\left(\frac\pi2\right)=\pi ab`

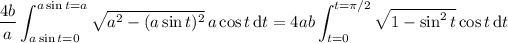
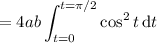
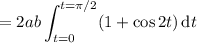
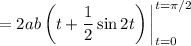
The integral with respect to
`y` can be resolved in a similar way.

###

We also could have converted to polar coordinates first, parameterizing the region
`E` by

`\begin{cases}x=ar\cos t\\y=br\sin t\\0\le r\le1\\0\le t\le2\pi\end{cases}`

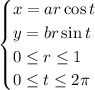
The Jacobian matrix for this transformation is

`\mathbf J=\begin{bmatrix}(\partial x)/(\partial r)&(\partial x)/(\partial t)\\\\(\partial y)/(\partial r)&(\partial y)/(\partial t)\end{bmatrix}=\begin{bmatrix}a\cos t&-ar\sin t\\b\sin t&br\cos t\end{bmatrix}`

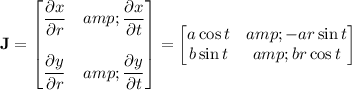
and its determinant gives
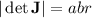`|\det\mathbf J|=abr`. So the integral reduces to

`\displaystyle\iint_E\mathrm dx\,\mathrm dy=\iint_E|\det\mathbf J|\,\mathrm dr\,\mathrm dt=ab\int_(t=0)^(t=2\pi)\int_(r=0)^(r=1)r\,\mathrm dr\,\mathrm dt`

`=\displaystyle\frac{ab}2\int_(t=0)^(t=2\pi)\mathrm dt`

`=\frac{ab}2(2\pi)=\pi ab`