Question

Given: Circle k(O), O∈

PL

KE
- tangent at E
KE=18, PL=15
Find: KP

Answer 1

I already did this question once so I'm just gonna include the answer

Answer 2

Answer: The value of KP = 12 units.

Explanation:

Since we have given that

KE is a tangent with KE = 18

KPL is a secant with PL = 15

Let KP = x

Since we know that The product of segments of secants is square of the tangents.

Mathematically, it is expressed as ,

`KE^2=KP.KL\\\\18^2=x(x+15)\\\\324=x^2+15x\\\\x^2+15x-324=0\\\\x^2+27x-12x-324=0\\\\x(x+27)-12(x+27)=0\\\\(x+27)(x-12)=0\\\\x=-27,x=12`

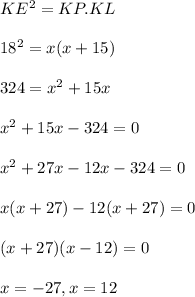
Measure of secant can't be negative.

So, KP = 12