Question

Use the table of values to write the exponential function

Answer 1

`(1)/(2)((1)/(4)^x)`

Explanation:

To find the function, compare the y values. Notice that each y value decreases by being divided by 4. This means the base of the exponential is 1/4.

To find the initial value, consider the point (0,0.5). When 1/4 is raised to the 0 power, the value is 1. This leaves that the initial value is 1/2 since 1/2*1 = 0.5.

The function is
`(1)/(2)((1)/(4)^x)`.

Answer 2

The required function is
`f(x)=(1)/(2)\left((1)/(4)\right)^x`.

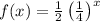Explanation:

The general exponential function is

`f(x)=ab^x` .... (1)

where, a is the initial value and b is growth factor.

From the given table it is clear that the function passes through the points (0,0.5) and (-1,2). It means the equation of function must be satisfied by the points (0,0.5) and (-1,2).

Substitute f(x)=0.5 and x=0 in equation (1), to find the value of a.

`0.5=ab^0`

`0.5=a`

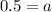
The value of a is 0.5.

Substitute a=0.5, f(x)=2 and x=-1 in equation (1), to find the value of b.

`2=(0.5)b^(-1)`

`2=(0.5)/(b)`

`2b=0.5`

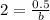
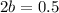
Divide both sides by 2.

`b=(0.5)/(2)`

`b=0.25`

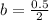
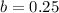
The value of b is 0.25.

Substitute a=0.5 and b=0.25 in equation (1).

`f(x)=0.5(0.25)^x`

`f(x)=(1)/(2)((1)/(4))^x`

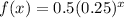
Therefore the required function is
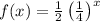`f(x)=(1)/(2)\left((1)/(4)\right)^x`.