Answer:
The volume of the figure is
![(l^(3))/(3)[(1)/(2)\pi-1]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9gci90pq6boluuevy7vmq8dix7qhz57oqu.png)
Explanation:
we know that
The volume of the figure is equal to the volume of the cone minus the volume of the square pyramid
step 1
Find the volume of the cone
The volume of the cone is equal to
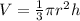
we have
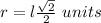

substitute
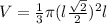

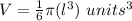
step 2
Find the volume of the square pyramid

we have
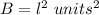

substitute
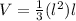
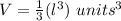
step 3
Find the difference
![(1)/(6)\pi (l^(3))-(1)/(3)(l^(3))=(l^(3))/(3)[(1)/(2)\pi-1]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bawfpzk9g7k0ktcgfv3fva1spkoqkjma75.png)