Question

A 60 kg gila monster on a merry go round is travelling in a circle with a radius of 3 m at a speed of 2m/s

What is acceleration and net force and compare this with monster weight

Answer 1

• Acceleration: 1.3 m/s².
• Net Force: 80 N (2 sig. fig.).
• Weight: 5.9 × 10² N = 590 N.

Step-by-step explanation

Apply the equation for objects that move in circles:

`a = (v^2)/(r)`,

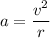where

• 
  `a` is the acceleration of the object,
• 
  `v` is the tangential speed of the object, and
• 
  `r` is the radius of the circular path.

For this monster:

• 
  `a` is to be found,
• 
  `v = 2\;m\cdot s^(-1)`, and
• 
  `r = 3\;\text{m}`.

`\displaystyle a = \frac{({2\;\text{m}\cdot\text{s}^(-1)})^(2)}{3\;\text{m}} = (2^2)/(3)\;\text{m}\cdot\text{s}^(-2)= 1.3\;\text{m}\cdot\text{s}^(-2)`.

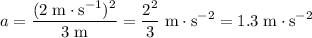By Newton's Second Law,

`\Sigma F = m\cdot a`,

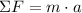where

• 
  `\Sigma F` is the net force on an object,
• 
  `m` is the mass of the object, and
• 
  `a` is the acceleration of the object.

• 
  `\Sigma F` is to be found,
• 
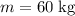  `m = 60\;\text{kg}` for this monster, and
• 
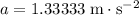  `a = 1.33333\;\text{m}\cdot\text{s}^(-2)` from previous calculations.

`\Sigma F = m\cdot a = 60\;\text{kg} * 1.33333\;\text{m}\cdot\text{s}^(-2) = 80\;\text{N}`.

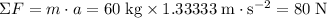Weight of an object near the surface of the earth:

`W = m\cdot g`,

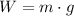where

• 
  `m` is the mass of the object, and
• 
  `g` is the gravitational acceleration "constant" (a.k.a. gravitational field strength.)
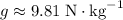  `g \approx 9.81\;\text{N}\cdot\text{kg}^(-1)` near the surface of the earth.

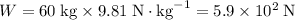`W = 60\;\text{kg} * 9.81\;\text{N}\cdot\text{kg}^(-1)=5.9* 10^(2) \;\text{N}`.