Question

To rationalize the denominator of 2/square 13+ squared 11 , you should multiply the expression by which fraction?

Answer 1

`\frac { \sqrt { 13 } - \sqrt { 11 } } { \sqrt { 13 } - \sqrt { 11 } }`

Step-by-step explanation:

We are given the following expression and we are to determine the expression that we need to multiply it with in order to rationalize the denominator:

`\frac { 2 } { \sqrt { 13 } + \sqrt { 11 } }`

To rationalize its denominator, we must multiply it with its conjugate.

For the denominator of the given expression, its conjugate would be
`\sqrt { 13 } - \sqrt { 11 }`.

So to rationalize the expression, we would multiply it with:

`\frac { \sqrt { 13 } - \sqrt { 11 } } { \sqrt { 13 } - \sqrt { 11 } }`

Answer 2

You should multiply the expression by
`(√(13)-√(11))/(√(13)-√(11))`

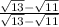
Step-by-step explanation:

To rationalize any expression, you must multiply it by its conjugate. A conjugate is defined as a similar expression to the original one but with an opposite sign

This means that:

The conjugate of a + b would be a - b

Now, the given expression is
`(2)/(√(13)+√(11))`

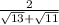
Consider the denominator:

From the above, we can conclude that the conjugate of
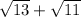`√(13)+√(11)` is
`√(13)-√(11)`

And, remember that we need to keep the value of the expression unchanged. This means that we must multiply both the numerator and the denominator by the same value

Therefore:

You should multiply the expression by
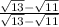`(√(13)-√(11))/(√(13)-√(11))` in order to rationalize the denominator

Hope this helps :)