Answer: 2500 years
Explanation:
I'm not quite sure if I'm doing this right myself but I'll give it a shot.
We use this formula to find half-life but we can just plug in the numbers we know to find t.
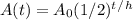
We know half-life is 5730 years and that the parchment has retained 74% of its Carbon-14. For
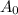 let's just assume that there are 100 original atoms of Carbon-14 and for A(t) let's assume there are 74 Carbon-14 atoms AFTER the amount of time has passed. That way, 74% of the C-14 still remains as 74/100 is 74%. Not quite sure how to explain it but I hope you get it. h is the last variable we need to know and it's just the half-life, which has been given to us already, 5730 years, so now we have this.
let's just assume that there are 100 original atoms of Carbon-14 and for A(t) let's assume there are 74 Carbon-14 atoms AFTER the amount of time has passed. That way, 74% of the C-14 still remains as 74/100 is 74%. Not quite sure how to explain it but I hope you get it. h is the last variable we need to know and it's just the half-life, which has been given to us already, 5730 years, so now we have this.
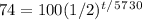
Now, solve. First, divide by 100.
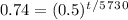
Take the log of everything

Divide the entire equation by log (0.5) and multiply the entire equation by 5730 to isolate the t and get
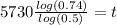
Use your calculator to solve that giant mess for t and you'll get that t is roughly 2489.128182 years. Round that to the nearest hundred years, and you'll find the hopefully correct answer is 2500 years.
Really hope that all the equations that I wrote came out good and that that's right, this is definitely the longest answer I've ever written.