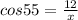Question

Can someone help I don’t understand this!?

Answer 1

A

Explanation:

Let's label what we currently have:

`Hypotenuse = x`

`Opposite = 12`

`Adjacent = ?`

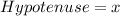
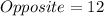
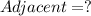
Since the answer choices are asking us to use cosine, we will need to use the cosine formula:

`cos=(adjacent)/(hypotenuse)`

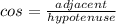
It seems like we don't have the adjacent side yet. However, if we use another angle, we can find out what x is. We know one angle is 35°. Since it is a right triangle, the other angle is 90°. Since all triangles add up to 180°, we know that the other angle is 55°. We CAN use cosine to find x if we use the 55° angle.

Let's label our new areas:

`Hypotenuse=x`

`Opposite=?`

`Adjacent=12`

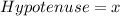
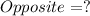
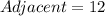
By using the cosine formula, we can now use the two values we have in the equation.

`cos 55=(12)/(x)`

Answer 2

to do this you need to know that cos= adjacent/hypotenous.

Therefore your answer would be cos55=12/x

Explanation: