Question

Which two values of x are roots of the polynomial below? x^2-11x+15

Answer 1

b and d

Explanation:

Answer 2

Answer: The correct options are

(B)
`x=(11+√(61))/(2).`

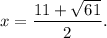
(D)
`x=(11-√(61))/(2).`

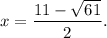
Step-by-step explanation: We are given to select the values of x that are the roots of the following polynomial :

`x^2-11x+15.`

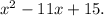
The quadratic equation formed by the given polynomial will be

`x^2-11x+15=0~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

we know that

the solution set of a quadratic equation
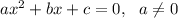`ax^2+bx+c=0,~~a\\eq 0` is given by

`x=(-b\pm√(b^2-4ac))/(2a).`

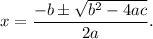
From equation (i), we have

a = 1, b = -11 and c = 15.

Therefore, the roots of equation (i) will be given by

`x=(-(-11)\pm√((-11)^2-4*1*15))/(2*1)\\\\\\\Rightarrow x=(11\pm√(121-60))/(2)\\\\\\\Rightarrow x=(11\pm√(61))/(2).`

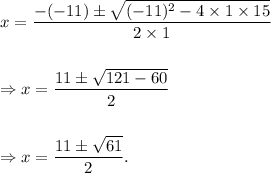
Thus, the roots of the given polynomial are

`x=(11+√(61))/(2),~~~~~x=(11-√(61))/(2).`

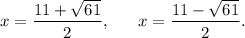
Options (B) and (D) are CORRECT.