Answer: The correct options are
(B)

(D)
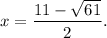
Step-by-step explanation: We are given to select the values of x that are the roots of the following polynomial :
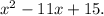
The quadratic equation formed by the given polynomial will be

we know that
the solution set of a quadratic equation
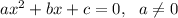 is given by
is given by
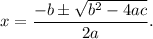
From equation (i), we have
a = 1, b = -11 and c = 15.
Therefore, the roots of equation (i) will be given by
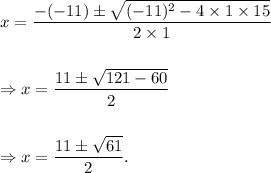
Thus, the roots of the given polynomial are
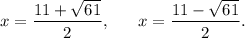
Options (B) and (D) are CORRECT.