Question

The perimeter of a rectangle is 88 m. If the width were doubled and the length were increased by 12 m, the perimeter would be 152 m. What is the length of the original rectangle?

Answer 1

Length of original rectangle = 24 m

Explanation:

Perimeter of rectangle

P = 2(l + b)

l - length and b - width

It is given that,the perimeter of a rectangle is 88 m. If the width were doubled and the length were increased by 12 m, the perimeter would be 152 m

Perimeter of original rectangle = 88 m

2(l + b) = 88

l + b = 44

b = 44 - l

To find length and width

length l = l + 12 and width = 2(44 - l) then,

Perimeter = 152 m

we can write,

2( l + 12 + 2(44 - l)) = 152

l + 12 + 88 - 2l = 152/2 = 76

100 - l = 76

l = 100 - 76 = 24

Therefore length = 24 m

width = 44 - l = 44 - 24 - 20 m

Answer 2

Answer: 24 meters.

Explanation:

The perimeter of a rectangle is given by the formula:

`P=2l+2w`

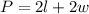
Where l is the lenght and w is the width.

The perimeter of the original rectangle is 88 m, then:

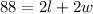`88=2l+2w` [EQUATION 1]

Where l is the length of the original rectangle

You know that if the width were doubled and the length were increased by 12 m, the perimeter would be 152 m. Therefore the new length is:

`l+12`

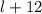
The new width is:

`2w`

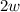
Susbtitute into the equation of the perimeter and solve for w:

`152=2(l+12)+2(2w)\\4w=152-(2l+24)`

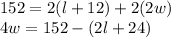
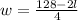`w=(128-2l)/(4)` [EQUATION 2]

Substitute the Equation 2 into Equation 1 and solve for the length, as you can see below:

`88=2l+2((128-2l)/(4))`

`88=2l+2((128-2l)/(4))\\88-2l=(128-2l)/(2)\\\\176-4l=128-2l\\176-128=4l-2l\\(48)/(2)=l\\\\24=l`

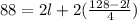
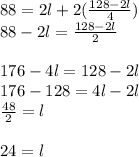
Therefore, the length of the original rectangle is 24 m.