Question

Find the surface area of the right square pyramid. Round your answer to the nearest hundredth. A 117.66 yd^2 B. 123.21 yd^2 C. 145.75 yd^2 D. 182.04 yd ^2

Answer 1

The correct answer option is C. 145.75 yd^2.

Explanation:

We are given a diagram of a right square pyramid with a slant height 11.1 yd, and base edge length 5.3 yd.

We know that the surface area of a right square pyramid is given by:

`(PI)/(2) +B`

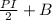
where P = perimeter of the base, I = slant height and B = base area.

Perimeter of base =
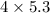`4 * 5.3` = 21.2 yd^2

Base Area =
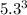`5.3^3` = 28.09 yd^2

Surface area of right square pyramid =
`(21.2 * 11.1 )/(2) + 28.09` = 145.75 yd^2

Answer 2

Answer: OPTION C

Explanation:

Use the following formula:

`SA=(pl)/(2)+B`

Where p is the perimeter of the base, l is the slant height and B is the area of the base.

The perimeter is:

`p=4*s=4*5.3yd=21.2yd`

Where s is the side lenght

The slant height is given:

`l=11.1yd`

The area of the base is:

`B=s^2=(5.3yd)^2=28.09yd^2`

Where s is the side lenght

Substitute values. Then, the result is:

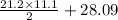`SA=((21.2yd)(11.1yd))/(2)+28.09yd^2)=145.75yd^2`