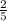Answer:
see explanation
Explanation:
Given f(x) = - 20x² + 23x - 6
To find the zeros set f(x) = 0, that is
- 20x² + 23x - 6 = 0 ( multiply through by - 1 )
20x² - 23x + 6 = 0
Consider the factors of the product of the coefficient of the x² term and the constant term which sum to give the coefficient of the x- term
product = 20 × 6 = 120 and sum = - 23
The factors are - 15 and - 8
Use these factors to split the x- term
20x² - 15x - 8x + 6 = 0 ( factor the first/second and third/fourth terms )
5x(4x - 3) - 2(4x - 3) = 0 ← factor out (4x - 3)
(4x - 3)(5x - 2) = 0
Equate each factor to zero and solve for x
4x - 3 = 0 ⇒ 4x = 3 ⇒ x =
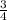
5x - 2 = 0 ⇒ 5x = 2 ⇒ x =