Answer:
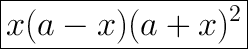
Explanation:
In order to factor this expression, our goal is to write the expression in a way that we can factor out a term.
With the expression
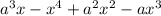 , we need to note an exponent rule.
, we need to note an exponent rule.
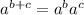
Step 1:
We can use this to get each term of this expression to have a term of
 so we can factor it out.
so we can factor it out.
Let's look at each term and get it so that we can factor out an x term.
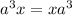 (Commutative Property)
(Commutative Property)
 (Since
(Since
 )
)
 (Since
(Since
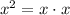 )
)
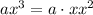 (Since
(Since

With this, our equation becomes
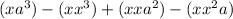 .
.
We now can factor out the common term x.

Step 2:
From here, we can now factor
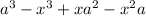
- Rearrange the equation:
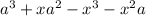
- Factor out
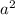 from
from
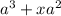 which comes out to be
which comes out to be

- Factor out
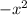 from
from
 which comes out to be
which comes out to be
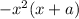
- We now have

- Factor out the common term,
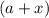 , which comes out to be
, which comes out to be

- Factor
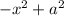 into
into
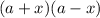
- We now have
 , which is simplified to
, which is simplified to

Finalizing:
Since we have just factored
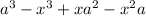 and factored x out of
and factored x out of
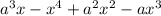 in the first couple of steps, we need to have it as a factorization of x.
in the first couple of steps, we need to have it as a factorization of x.
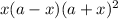
Hope this helped!