Question

$800 is deposited in an account that pays 9% annual interest compounded annually. Find the balance after four years

Answer 1

$1,129.27

Explanation:

Compounded interest formula is

`A=P(1+(r)/(n))^(nt)`

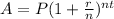
Where
`A` is the final amount,
`P` is the principal,
`r` is the anual interest in decimal,
`n` is the numer of compounded periods in one year and
`t` is the time in years.

`P=\$800\\r=0.09\\n=1\\t=4`

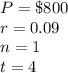
Notice that
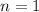`n=1`, because the interest is compounded anually, if the interest is compounded, then
`n=12`, because there would be 12 compound periods in one year.

Then, we replace all these vaules in the formula

`A=P(1+(r)/(n))^(nt)\\A=800(1+(0.09)/(1))^(1(4))=800(1.09)^(4)\\ A=1,129.26`

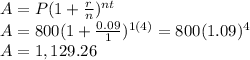
Therefore, after 4 years, the amount would be $1,129.27.