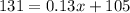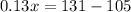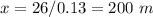Question

the price of a climbing trip to mount kilimanjaro includes an initial fee plus a constant fee per meter. the table compares the total distance of a trip (in meters) and the price of the trip (in dollars).

Answer 1

$0.13

Explanation:

Answer 2

`200\ m`

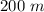
Explanation:

Let

x------> total distance of a trip

y-------> the price of a trip

step 1

Find the slope

Let

`A(70,114.1),B(100,118)`

`m=((118-114.1))/(100-70)=0.13(\$)/(m)`

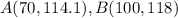
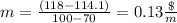
step 2

Find the equation of the line into point slope form

`y-y1=m(x-x1)`

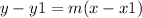
we have

`m=0.13`

`A(70,114.1)`

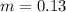
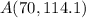
substitute

`y-114.1=0.13(x-70)`

`y=0.13x-9.1+114.1`

`y=0.13x+105`

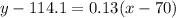
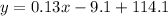
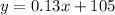
step 3

For
`y=\$131`

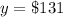
Find the value of x

substitute in the linear equation and solve for x

`131=0.13x+105`

`0.13x=131-105`

`x=26/0.13=200\ m`