Answer:
(i) Exponential Decay
(ii)linear
(iii)Exponential Growth
Explanation:
(i)
Cost of the van=$25,000.
After 2 years, value of van=$17,500.
After 4 years, value of van = $12,250.
Its a decay but to be a exponential decay it must have constant rate.
As its known the exponential decay formula is
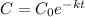
Now substitute the values in the above formula
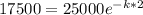
Now on simplification, we get
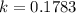
Now again apply the same formula for the next time interval
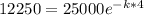
Now on simplification, we get
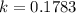
Since the value of k is constant for both the time interval. Hence the decays is exponential.
(ii)
At the beginning, battery life=100%.
After 3 Hours, battery life=60%.
After 6 Hours, battery life = 20%.
Since the value of battery life decreases by 40% in each interval. Hence the decay of battery life is linear.
(iii)
Initial population=20.
After 5 years, population=30.
After 10 years, population = 45.
Its a growth but to be a exponential growth it must have constant rate.
As its known the exponential growth formula is
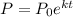
Now substitute the values in the above formula

Now on simplification, we get
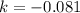
Now again apply the same formula for the next time interval
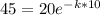
Now on simplification, we get
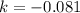
Since the value of k is constant for both the time interval. Hence the decays is exponential.