Question

(x^(2))/(9)+(y^(2))/(49)=1 The distance from the center to the major intercept is

Answer 1

b = 7 units.

Explanation:

The given equation of the ellipse is

`(x^(2) )/(9) +(y^(2) )/(49)=1`

As we know in an ellipse
`(x^(2) )/(a^(2) )+ (y^(2) )/(b^(2))=1`

a will be major axis and b is the minor axis when ( a > b )

In the given equation 49 > 9 ⇒ b² > a²

so major axis will be = √49

= 7

Therefore, distance from center to the major intercept is b = 7 units.

Answer 2

7

Explanation:

This is an equation of an ellipse of the form:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

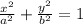
Where a and b are the minor and major intercepts, given a<b

In this question, a<b and a = 3 and b = 7

The distance from the center to the major intercept is b, thus the distance we are seeking for is 7