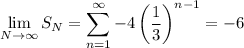a. The series is
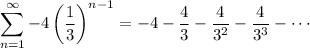
(first four terms are listed)
b. The series converges because this is a geometric series with
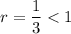 .
.
c. Let
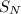 be the
be the
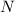 -th partial sum of the series:
-th partial sum of the series:
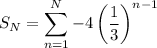
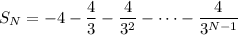
Multiplying both sides by
 gives
gives
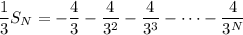
Subtracting this from
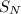 gives
gives
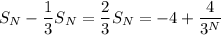
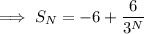
As
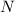 gets larger and larger
gets larger and larger
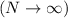 the rational term converges to 0 and we're left with
the rational term converges to 0 and we're left with