Question

A car travels 2 5/8 miles in 3 1/2 minutes at a constant speed. Which equation represents the distance, d, that the car travels in m minutes?

Answer 1

`d=0.75m`

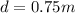
Explanation:

Let

d------> the distance in miles

m----> the time in minutes

we know that

The speed is equal to divide the distance by the time

so

`speed=d/m`

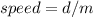
we have

`d=2(5)/(8)\ miles=(2*8+5)/(8)=(21)/(8)\ miles`

`m=3(1)/(2)\ minutes=(3*2+1)/(2)=(7)/(2)\ minutes`

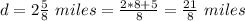
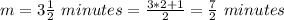
we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
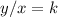`y/x=k` or
`y=kx`

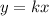
so

In this problem the speed is the constant of proportionality

`d=km`

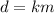
Find the value of k

`k=((21/8))/((7/2)) =0.75(miles)/(minute)`

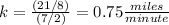
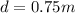`d=0.75m` ----> linear equation that represent the distance, d, that the car travels in m minutes