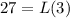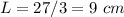Question

The rectangle shown has an area of 27 cm2 and is modeled by the equation A = 2w2 + 3w, where w is the width. What is the length of the rectangle?

Answer 1

The length of the rectangle is
`9\ cm`

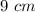
Explanation:

we know that

The area of rectangle is equal to

`A=LW`

In this problem we have

`A=27\ cm^(2)`

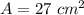
so

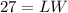`27=LW` ------> equation A

and

`A=2w^(2)+3w`

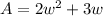
so

`27=2w^(2)+3w`

`2w^(2)+3w-27=0`

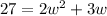
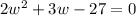
The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`2w^(2)+3w-27=0`

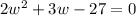
so

`a=2\\b=3\\c=-27`

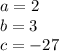
substitute in the formula

`w=\frac{-3(+/-)\sqrt{3^(2)-4(2)(-27)}} {2(2)}`

`w=\frac{-3(+/-)√(225)} {4}`

`w=\frac{-3(+/-)15} {4}`

`w=\frac{-3(+)15} {4}=3`

`w=\frac{-3(-)15} {4}=-4.5`

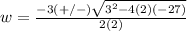
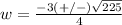
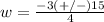
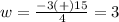
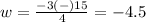
The solution of the quadratic equation is

`w= 3\ cm`

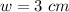
Find the value of L

`27=L(3)`

`L=27/3=9\ cm`