Question

Use a graphing calculator and a system of equations to find the roots of the equation. x4 − 4x3 = 6x2 − 12x From least to greatest, what are the integral roots of the equation?

answer is -2,0

Answer 1

The roots are -2 , 0 , (3 - √3) , (3 + √3)

The integral roots are -2 , 0

Explanation:

∵ x^4 - 4x³ = 6x² - 12x

∴ x^4 - 4x³ - 6x² + 12x = 0

∴ x(x³ - 4x² - 6x + 12) = 0

∴ x = 0

∴ x³ - 4x² - 6x + 12 = 0

∵ f(-2) = (-2)³ - 4(-2)² - 6(-2) + 12 = -8 - 16 + 12 + 12 = 0

∴ (x + 2) is a factor of the equation x³ - 4x² - 6x + 12 = 0

∴ (x³ - 4x² - 6x + 12) ÷ (x + 2) = (x² - 6x + 6)(x + 2)

∴ (x² - 6x + 6)(x + 2) = 0

∴ x + 2 = 0 ⇒ ∴ x = -2

∴ x² - 6x + 6 = 0 ⇒ quadratic equation (ax² + bx + c = 0)

∵ a = 1 , b = -6 , c = 6

∵
`x=\frac{-b+\sqrt{b^(2)-4ac}}{2a}=(6+√(36-24))/(2)=(6+2√(3))/(2)=3+√(3)`

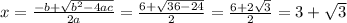
∴ x = 3 + √3 and x = 3 - √3

∴ The roots are -2 , 0 , (3 - √3) , (3 + √3)

Answer 2

The roots are x=0 or x=−2 or x=4.73 or x=1.26

Explanation:

Let's solve your equation step-by-step.

x4−4x3=6x2−12x

Step 1:

Subtract 6x^2-12x from both sides.

x4−4x3−(6x2−12x)=6x2−12x−(6x2−12x)

x4−4x3−6x2+12x=0

Step 2:

Factor left side of equation.

x(x+2)(x2−6x+6)=0

Step 3:

Set factors equal to 0.

x=0 or x+2=0 or x2−6x+6=0

x=0 or x=−2 or x=4.73 or x=1.26

Answer:

x=0 or x=−2 or x=4.73 or x=1.26