Answer:
The roots are -2 , 0 , (3 - √3) , (3 + √3)
The integral roots are -2 , 0
Explanation:
∵ x^4 - 4x³ = 6x² - 12x
∴ x^4 - 4x³ - 6x² + 12x = 0
∴ x(x³ - 4x² - 6x + 12) = 0
∴ x = 0
∴ x³ - 4x² - 6x + 12 = 0
∵ f(-2) = (-2)³ - 4(-2)² - 6(-2) + 12 = -8 - 16 + 12 + 12 = 0
∴ (x + 2) is a factor of the equation x³ - 4x² - 6x + 12 = 0
∴ (x³ - 4x² - 6x + 12) ÷ (x + 2) = (x² - 6x + 6)(x + 2)
∴ (x² - 6x + 6)(x + 2) = 0
∴ x + 2 = 0 ⇒ ∴ x = -2
∴ x² - 6x + 6 = 0 ⇒ quadratic equation (ax² + bx + c = 0)
∵ a = 1 , b = -6 , c = 6
∵
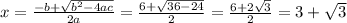
∴ x = 3 + √3 and x = 3 - √3
∴ The roots are -2 , 0 , (3 - √3) , (3 + √3)