Answer:
Option B. is the answer.
Explanation:
In the given picture we have to prove that quadrilateral HIJK is a kite.
1. For a kite quadrilateral HIJK will be a kite, if it's sides IJ = IH
From the graph length of I H = 4 - 1 = 3 units
Length of IJ = 0 - (-3) = 3 units
Therefore, IJ = IH = 3 units
2. Sides HK should be equal to JK
Length of HK =
![\sqrt{[1-(-1)]^(2)+[2-(-3)^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9ohb2p5ocwsrx13lgqhmrh1lbwgjhvn635.png) by Pythagoras Theorem
by Pythagoras Theorem
=

Similarly length of JK =
![\sqrt{(2)^(2)+[4-(-1)]^(2)}=\sqrt{4+5^(2) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/so67bdz2s3jub64zpxtn2p4uih7whnfj1j.png)
=
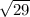
Therefore HK = JK = √29 units
3). IH ≠ JK and ij ≠ HK
All these conditions are fulfilled for HIJK to be a kite.
Option B. is the answer.