Question

A weather balloon is filled with helium that occupies a volume of 5.57 104 L at 0.995 atm and 32.0°C. After it is released, it rises to a location where the pressure is 0.720 atm and the temperature is -14.5°C. What is the volume of the balloon at that new location?

Answer 1

6.52 × 10⁴ L. (3 sig. fig.)

Step-by-step explanation

Helium is a noble gas. The interaction between two helium molecules is rather weak, which makes the gas rather "ideal."

Consider the ideal gas law:

`P\cdot V = n\cdot R\cdot T`,

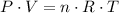where

• 
  `P` is the pressure of the gas,
• 
  `V` is the volume of the gas,
• 
  `n` is the number of gas particles in the gas,
• 
  `R` is the ideal gas constant, and
• 
  `T` is the absolute temperature of the gas in degrees Kelvins.

The question is asking for the final volume
`V` of the gas. Rearrange the ideal gas equation for volume:

`V = (n \cdot R \cdot T)/(P)`.

Both the temperature of the gas,
`T`, and the pressure on the gas changed in this process. To find the new volume of the gas, change one variable at a time.

Start with the absolute temperature of the gas:

• 
  `T_0 = (32.0 + 273.15) \;\text{K} = 305.15\;\text{K}`,
• 
  `T_1 = (-14.5 + 273.15) \;\text{K} = 258.65\;\text{K}`.

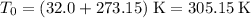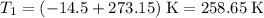The volume of the gas is proportional to its temperature if both
`n` and
`P` stay constant.

• 
  `n` won't change unless the balloon leaks, and
• consider
  `P` to be constant, for calculations that include
  `T`.

`V_1 = V_0 \cdot (T_1)/(T_2) = 5.57* 10^(4)\;\text{L}* \frac{258.65\;\textbf{K}}{305.15\;\textbf{K}} = 4.72122* 10^(4)\;\text{L}`.

Now, keep the temperature at
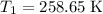`T_1 =258.65\;\text{K}` and change the pressure on the gas:

• 
  `P_1 = 0.995\;\text{atm}`,
• 
  `P_2 = 0.720\;\text{atm}`.

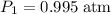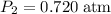The volume of the gas is proportional to the reciprocal of its absolute temperature
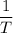`(1)/(T)` if both
`n` and
`T` stays constant. In other words,

`V_2 = V_1 \cdot((1)/(P_2))/((1)/(P_1)) = V_1\cdot(P_1)/(P_2) = 4.72122* 10^(4)\;\text{L}*\frac{0.995\;\text{atm}}{0.720\;\text{atm}}=6.52* 10^(4)\;\text{L}`

(3 sig. fig. as in the question.).

See if you get the same result if you hold
`T` constant, change
`P`, and then move on to change
`T`.