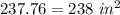Question

A regular pentagon has radii of 10 inches. What is its area of the pentagon, rounded to the nearest whole square inch?

Answer 1

`238\ in^(2)`

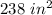
Explanation:

we know that

The radii divide the pentagon into five isosceles triangles each with a center angle of 360/5 = 72 degrees

so

The area of the regular pentagon is equal to the area of one isosceles triangle multiplied by 5

step 1

Find the area of one isosceles triangle

Applying the law of sines

`A=(1)/(2)(10)(10)sin(72\°)=47.55\ in^(2)`

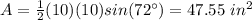
step 2

Find the area of the regular pentagon

`47.55*(5)=237.76\ in^(2)`

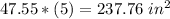
Round to the nearest whole square inch

`237.76=238\ in^(2)`