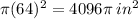Question

A circle has an area of 256 square inches. If the radius of

the circle is multiplied by 4, what will be the area of the new
circle formed?
OA) 890 in.
OB) 1520 in.
OC) 4096 in
OD 5360 in.

Answer 1

Answer: C

Explanation:

Answer 2

Option C (4096π in²)

Explanation:

Area of the circle = 256π in²

We know that
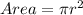`Area=\pi r^(2)` , where r = radius of the circle

So,

`256\pi = \pi r^(2)`

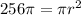
Cancelling π from both the sides,

`=> r^(2) = 256`

`=> r = √(256) = 16`

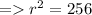
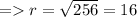
The radius of the circle = 16 in.

When the radius is multiplied with 4 , new radius = 16×4 = 64 in.

New Area =
`\pi (64)^(2) =4096\pi \: in^(2)`