Question

HELP!!!

The depreciating value of a semi-truck can be modeled by y = Ao(0.79)x, where y is the remaining value of the semi, xis the time in years, and it depreciates at 21% per year. ​

Answer 1

`\$77,000` and the graph would fall at a slower rate to the right

Explanation:

we have

`y=Ao(0.79)^(x)`

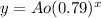
Observing the graph

The initial value Ao of the truck is equal to the y-coordinate of the y-intercept of the graph

so

`Ao=\$77,000`

If the depreciation rate was 15% per year, the new formula would be

`y=Ao(1-0.15)^(x)`

`y=Ao(0.85)^(x)`

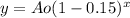
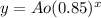
`y=77,000(0.85)^(x)` ----> the graph would fall at a slower rate to the right

using a graphing tool

compare the graphs