Hello!
The answer is:
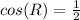
Why?
Since it's a right triangle and we need to know the adjacent side of the triangle, in order to find cos(R), we can use the Pythagorean Theorem.
Pythagorean Theorem formula:
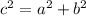
Where:
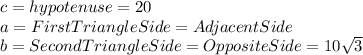
So, the adjacent side will be:
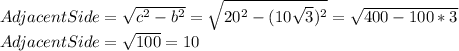
Now, that we know the adjacent side, we can calculate cos(R), so:
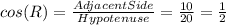
Have a nice day!