Question

Find the standard deviation of the sample data set.

127 135 128 131 133 127 122

A.
4.4

B.
4.0

C.
19.0

D.
2.0

Answer 1

the answer is B

Explanation:

Answer 2

Option A) 4.4 is the correct standard deviation of the the given data set.

Explanation:

We are given the following data set:

127, 135, 128, 131, 133, 127, 122

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

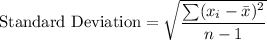
where
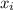`x_i` are data points,
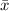`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

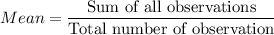
Solving:

`Mean =\displaystyle(903)/(7) = 129`

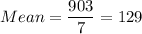
Sum of squares of differences = 4 + 36 + 1 + 4 + 16 + 4 + 49 = 114

`S.D = \sqrt{(114)/(6)} = 4.358898944 \approx 4.4`

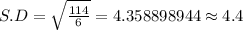
Option A) is the correct standard deviation of the the given data set.